In 1874, Kohlrausch formulated the law of independent migration of ions based on the experimental data of conductivities of various electrolytes. This law can be stated as follows:
At infinite dilution, the dissociation of the electrolyte is complete and hence each ion makes definite contribution to the equivalent conductivity of the electrolyte irrespective of the nature of other ions associated with it.
Therefore the limiting equivalent conductivity of an electrolyte is the algebraic sum of limiting equivalent conductivities of its constituent ions.
i.e., The limiting equivalent conductivity of an electrolyte, Λoelectrolyte
![]()
Where λo+ and λo- are the limiting equivalent conductivities of cation and anion respectively.
However the Kohlrausch law can also be stated in terms of molar conductivities as:
The limiting molar conductivity of an electrolyte is the sum of individual contributions of limiting molar conductivities of its constituent ions.
i.e., The molar equivalent conductivity of an electrolyte, μoelectrolyte
![]()
Where μo+ and μo- are the limiting molar conductivities of cation and anion respectively.
And n+ and n- are the stoichiometric numbers of positive and negative ions formed during the dissociation of electrolyte.
Kohlrausch observed that at infinite dilutions, the difference between the conductivities of sodium and potassium salts is constant irrespective of the associated anions, as tabulated below.
| Salt pair | Conductivity
(mho cm2 equiv) |
Difference |
| NaCl | 108.90 | 21.20 |
| KCl | 130.10 | |
| NaNO3 | 105.33 | 21.17 |
| KNO3 | 126.50 | |
| NaBr | 111.10 | 21.20 |
| KBr | 132.30 |
Kohlrausch argued that the constant difference in the conductivities of above pairs can be ascribed to the fact that the mobility of sodium and potassium ions at infinite dilution is not influenced by the nature of counter ions. The ions at such a low concentration migrate in the electric field as they are independent i.e., they show same ionic conductance irrespective of the nature of counter ion.
1) Calculation of limiting conductivities of weak electrolytes: The Kohlrausch law can be used to calculate the limiting conductivities of weak electrolytes.
E.g., The calculation of limiting equivalent conductance of acetic acid, a weak electrolyte is illustrated below.
According to Kohlrausch law, the limiting equivalent conductance values of CH3COOH, CH3COONa, HCl and NaCl can be written as follows:
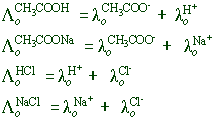
Therefore
![]()
2) Determination of degree of ionization (α) of weak electrolyte: The degree of ionization of a weak electrolyte at a particular concentration is equal to the ratio of actual number of ions formed due to partial ionization to the expected number of ions formed upon complete dissociation.
![]()
Since the conductance is proportional to the number of ions in the solution, the degree of ionization is equal to the conductance ratio as given below.
![]()
Where
Λc= equivalent conductivity at given concentration.
Λo= limiting equivalent conductivity.
λo+ = limiting equivalent conductivity of cation.
λo- = limiting equivalent conductivity of anion.