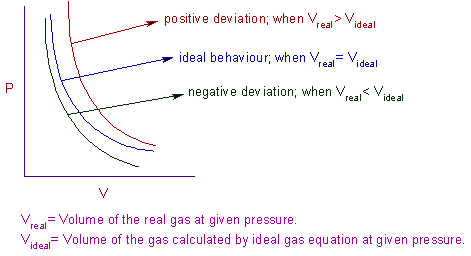
Real gases do not obey ideal gas equation under all conditions. They nearly obey ideal gas equation at higher temperatures and very low pressures. However they show deviations from ideality at low temperatures and high pressures.
The deviations from ideal gas behaviour can be illustrated as follows:
The isotherms obtained by plotting pressure, P against volume, V for real gases do not coincide with that of ideal gas, as shown below.

It is clear from above graphs that the volume of real gas is more than or less than expected in certain cases. The deviation from ideal gas behaviour can also be expressed by compressibility factor, Z.
The ratio of PV to nRT is known as compressibility factor.
(or)
The ratio of volume of real gas, Vreal to the ideal volume of that gas, Vperfect calculated by ideal gas equation is known as compressibility factor.
![]()
But from ideal gas equation:
PVperfect = nRT
or
![]()
Therefore
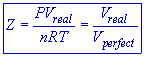
* For ideal or perfect gases, the compressibility factor, Z = 1.
* But for real gases, Z ≠1.
Case-I : If Z>1
* Vreal > Videal
* The repulsion forces become more significant than the attractive forces.
* The gas cannot be compressed easily.
* Usually the Z > 1 for so called permanent gases like He, H2 etc.
Case-II: If Z < 1
* Vreal < Videal
* The attractive forces are more significant than the repulsive forces.
* The gas can be liquefied easily.
* Usually the Z < 1 for gases like NH3, CO2, SO2 etc.
The isotherms for one mole of different gases, plotted against the Z value and pressure, P at 0 oC are shown below:
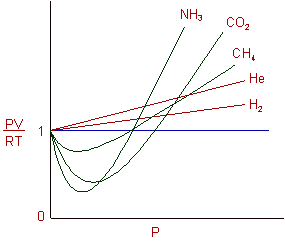
* For gases like He, H2 the Z value increases with increase in pressure (positive deviation).
It is because, the repulsive forces become more significant and the attractive forces become less dominant. Hence these gases are difficult to be condensed.
* For gases like CH4, CO2, NH3 etc., the Z value decreases initially (negative deviation) but increases at higher pressures.
It is because: at low pressures, the attraction forces are more dominant over the repulsion forces, whereas at higher pressures the repulsion forces become significant as the molecules approach closer to each other.
* But for all the gases, the Z value approaches one at very low pressures, indicating the ideal behaviour.
Also consider the following graphs of Z vs P for a particular gas, N2 at different temperatures.
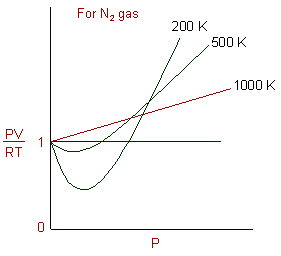
In above graphs, the curves are approaching the horizontal line with increase in the temperature i.e., the gases approach ideal behaviour at higher temperatures.
The deviations from ideal gas behaviour can be ascertained to the following faulty assumptions by kinetic theory of gases.
* The real volume of the gas molecules is negligible when compared to the volume of the container.
* There are no forces of attraction or repulsion between the gas molecules.
Hence van der Waal suggested the following corrections:
* The gas molecules possess finite volume and hence should not be neglected. It is especially true at high pressures and low temperatures and should be accounted for.
* In case of real gases, both the forces of attraction as well as repulsion operate between gas molecules.
Note: If the gases obey the kinetic theory of gases, then they cannot be compressed since the attractions between the gas molecules is negligible.
Also the following corrections are applied by van der Waals to the ideal gas equation:
The volume available for the gas molecules is less than the volume of the container, V.
The available volume is obtained by subtracting excluded volume of ‘n’ moles of gas, nb from the volume of the container.
Available volume = V - nb
Where 'b' is a constant characteristic of a gas.
The ideal gas equation can be written after correcting for this as:
P(V-nb) = nRT
The pressure of the real gas is less than the expected pressure due to attractions between the molecules. These attractions slow down the motion of gas molecules and result in:
i) reduction of frequency of collissions over the walls and
ii) reduction in the force with which the molecules strike the walls.
Hence
Pideal = Preal + p
Where p = reduction in pressure
However the reduction in pressure is proportional to the square of molar concentration, n/V.
![]()
One factor for reduction in frequency of collisions and the second factor for reduction in strength of their impulses on the walls.
or
![]()
where ‘a’ is a proportionality constant characteristic of a gas.
Therefore:
![]()
Now the ideal gas equation can be modified once again by introducing this pressure correction as:
![]()
This is known as van der Waals equation of state.
For one mole of a gas, the equation can be written as:
![]()
Where Vm = volume occupied by one mole of a real gas
Remember that:
P = observed pressure of the real gas
whereas,![]()
V = volume occupied by the real gas and is equal to the volume of the container.
whereas, (V - nb) = available volume for gas molecules
Units of ‘a’ and ‘b’:
For ‘a’ ----------- atm L2 mol-2
For ‘b’ ----------- L. mol-1
* ‘a’ is called van der Waals constant of attraction. Higher values of ‘a’ indicate greater attraction between gas molecules. The easily compressible gases like ammonia, HCl possess higher ‘a’ values.
Greater the value of ‘a’ for a gas easier is the liquefaction.
* ‘b’ is called excluded volume of the gas.
![]()
Where NA = Avogadro number and r = radius of molecule
* For a given gas, the numerical value of ‘a’ is greater than that of ‘b’.
* The Boyle's temperature (TB) and inversion temperature (Ti) are related to the two van der Waals constants as:
![]()
Note:
Boyle’s temperature is the temperature at which the gases obey the ideal gas laws over a wide range of pressures.
Inversion temperature is the temperature at which the Joule Thompson coefficient changes its sign i.e., from positive to negative or vice versa.
Van der Waals considered the gas molecules are hard spheres which are not penetrated by other molecules. Consider two hard spheres of radius ‘r’ in closest contact are enveloped by a sphere of radius ‘d’ that is forbidden for the centers of the other particles.
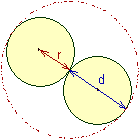
Hence the volume excluded for the third sphere is given by:
![]()
However the volume excluded by one particle is:
![]()
Therefore the volume excluded by NA particles, b is given by:
![]()
Note: This factor four is considered erroneous by Maxwell and proposed that the excluded volume is 16 times of the volume of NA molecules.
At low pressures: Since V is large and therefore ‘b’ is negligible compared to V, the van der Waals equation for one mole of a gas is reduced to:
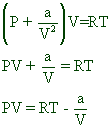
* Note that V = Vm = molar volume.
Therefore: PV < RT at lower pressures. This is the reason for decrease in the Z value at low pressures.
Note: By dividing with RT on each side, the above equation can be written as:
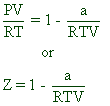
At very low pressures: Since V is very large and therefore both ‘b’ and ‘a/V2’ values become negligible. Hence the van der Waals equation for one mole of gas is reduced to:
PV = RT
Therefore, at very low pressures all the gases obey the ideal gas equation.
At high pressures: Since the volume of the gas is small, the value of ‘b’ cannot be neglected. Although a/V2 is also large its value may be neglected in comparison with very high value of P. Hence the van der Waals equation is reduced to:
P(V - b) = RT
PV - Pb = RT
PV = RT + Pb
Therefore: at high pressures, PV > RT. This explains the raising parts of the isotherms, at high pressures, plotted between Z vs P.
Note: By dividing with RT on each side, the above equation can be written as:
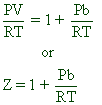
At high temperatures: In this case, V is very large and attractions are negligible. Hence both ‘b’ and ‘a/V2’ are negligible. This reduces the van der Waals equation to:
PV = RT for one mole
For H2 and He gases: Since the actual volume of these gas molecules is very small, the intermolecular forces of attractions are very small. i.e., a/V2 can be ignored. Thus the van der Waals equation is reduced to:
P(V - b) = RT
PV - Pb = RT
PV = RT + Pb
Therefore, for H2 and He gases, PV > RT. Hence for these gases, the Z value is always greater than one as evident from the isotherms plotted between Z vs P.
* The Vander Waal's equation holds good for real gases up to moderately high pressures.
* It explains the isotherms of PV/RT vs P for various gases.
* From this equation it is possible to obtain expressions for Boyle's temperature, critical constants and inversion temperature in terms of the Vander Waal's constants 'a' and 'b'.
Liquefaction of gases: The isotherms plotted between P vs V at different temperatures for one mole of CO2 gas are shown below.
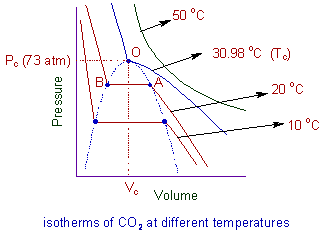
Following conclusions can be drawn from these graphs:
* At higher temperatures, say 50 oC, the isotherms show ideal behaviour.
* As the temperature is lowered, the isotherms show deviation from ideal behaviour.
* At 30.98 oC, carbon dioxide remains as gas up to 73 atm. But liquid appears for the first time at 73 atm (represented by point ‘O’). Hence 30.98 oC is called critical temperature for CO2.
And above 73 atm. there is a steep rise in the pressure. This steep portion of the curve represents the isotherm of liquid state for which small decrease in volume results in steep rise in the pressure.
* At even lower temperature, 20 oC, the liquid appears at point ‘A’. Further compression does not change the pressure up to point ‘B’. After point, B the curve again becomes steep representing the isotherm for liquid CO2.
Critical Temperature (Tc): It is the temperature above which a gas cannot be liquefied by applying pressure.
![]()
Critical Pressure (Pc): It is the minimum pressure required to cause liquefaction at critical temperature, Tc.
![]()
Critical Volume (Vc): It is the volume occupied by one mole of a gas at Tc and Pc.
Vc = 3b
Super critical fluid: The dense fluid obtained by compressing a gas above its critical temperature is called super critical fluid.
* It is not a liquid though its density is similar to that of liquid.
* It is not a gas due to high density and no distinct surface that separates it from the vapour phase.
* It can be used as a solvent.
E.g. The super critical fluid of CO2 is used in the extraction of caffeine from coffee beans.