Theorem: In a nonlinear molecule, if degenerate orbitals are asymmetrically occupied, a distortion will occur to remove the degeneracy.
(or)
In an electronically degenerate state, a nonlinear molecule undergoes distortion to remove the degeneracy by lowering the symmetry and thus by lowering the energy.
WATCH THE FOLLOWING VIDEO FOR ANIMATED INTRODUCTION ON JAHN-TELLER DISTORTION.
What is electronically degenerate state?
An electronically degenerate state represents the availability of more than one degenerate orbitals for an electron. In this condition the degenerate orbitals are said to be asymmetrically occupied.
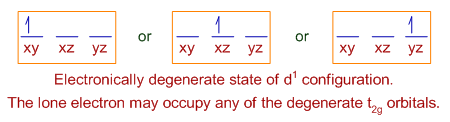
E.g. In octahedral symmetry, the d1 configuration is said to be electronically degenerate since three t2g orbitals with same energy are available for the electron to occupy. In this condition, the degenerate orbitals are also said to be asymmetrically occupied by electrons.

Whereas the d3 configuration in octahedral geometry is non-degenerate and symmetric. It is not possible to put two electrons in one orbital, which is against of Hund's rule of maximum multiplicity.

And remember that, Jahn Teller effect is observed for metal ions with electronically degenerate states.
* In the electronically degenerate state, the orbitals are said to be asymmetrically occupied and hence get more energy. Therefore, the system tries to get rid of extra energy by lowering the overall symmetry of the molecule i.e., undergoing distortion, which is otherwise known as Jahn Teller distortion (effect).
E.g. In case of octahedral d9 configuration, the last electron may occupy either dz2 or dx2-y2 orbitals of eg set. If it occupies dz2 orbital, most of the electron density will be concentrated between the metal and the two ligands on the z axis. Thus, there will be greater electrostatic repulsion associated with these ligands than with the other four on xy plane. This asymmetric distribution of the electron density may increase the overall energy of the system. To get rid of this, the complex suffers elongation of bonds on z-axis and thus lowers the symmetry.
Conversely, occupation of the dx2-y2 orbital would lead to elongation of bonds along the x and y axes.
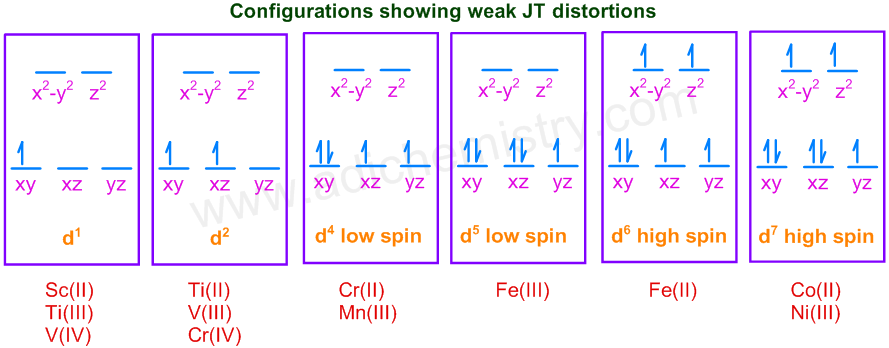
* The Jahn Teller effect is mostly observed in octahedral environments. Theoretically the electronic degeneracy in octahedral symmetry is possible in all the configurations except d3, d8, d10, high spin d5 and low spin d6 configurations.
However, considerable distortions are usually observed in high spin d4 , low spin d7 and d9 configurations in the octahedral environment. It is because the Jahn Teller distortion is usually significant for asymmetrically occupied eg orbitals since they are directed towards the ligands and the energy gain is considerably more.
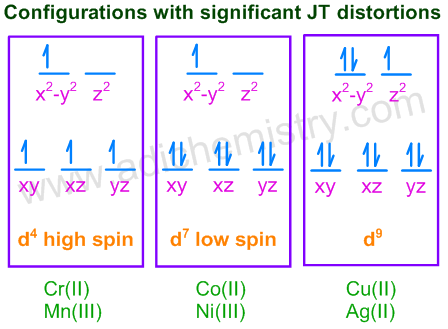
* In case of unevenly occupied t2g orbitals, the Jahn Teller distortion is very weak since the t2g set does not point directly at the ligands and therefore the energy gain is much less.
E.g. d1; d2; low spin d4 & d5; high spin d7 & d7 configurations.
Because of same reason, the tetrahedral complexes also do not exhibit Jahn-Teller distortion. Again, in this case also the ligands are not pointing towards the orbitals directly and hence there is less stabilization to be gained upon distortion.
Note: The Jahn-Teller distortion in case of low spin d8 octahedral systems to give square planar complexes as explained by some authors is controversial. This will be discussed in later sections.
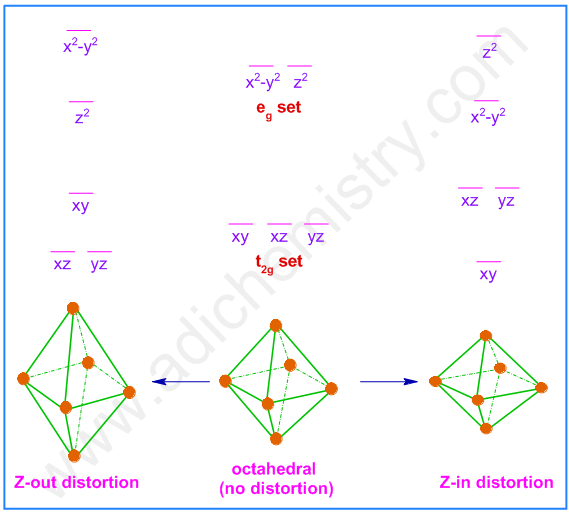
* The degeneracy of orbitals can be removed by lowering the symmetry of molecule. This can be achieved by either elongation of bonds along the z-axis (Z-out distortion) or by shortening the bonds along the z-axis (Z-in distortion). Thus an octahedrally symmetrical molecule is distorted to tetragonal geometry.
Z-out Jahn-Teller distortion: In this case, the energies of d-orbitals with z factor ( i.e., dz2, dxz, dyz ) are lowered since the bonds along the z-axis are elongated. This is the most preferred distortion and occurs in most of the cases, especially when the degeneracy occurs in eg level.
E.g. Usually the octahedral d2, d4 high spin, d7 low spin, d8 low spin & d9 configurations show the z-out distortion.
Theoretically it is not possible to predict the type of distortion occurs when the degeneracy occurs in eg level. However it is observed that z-out distortion is more preferred.
Z-in Jahn-Teller distortion: In this case the energies of orbitals with z factor are increased since the bonds along the z-axis are shortened. This type of distortion is observed in case of octahedral d1 configuration. The only electron will now occupy the dxy orbital with lower energy.
E.g. The octahedral d1 configurations like Ti(III) in [Ti(H2O)6]3+ can show z-in distortion (theoretically?). In this case, the z-out distortion do not remove the degeneracy since even after distortion there are still two degenerate orbitals i.e., dxz and dyz available for the electron to occupy. See the following diagram.
Also remember that the Jahn-Teller theorem does NOT predict how large a distortion should occur.
Static Jahn-Teller distortion: Some molecules show tetragonal shape under all conditions i.e., in solid state and in solution state; at lower and relatively higher temperatures. This is referred to as static Jahn-Teller distortion. It is observed when the degeneracy occurs in eg orbitals. Hence the distortion is strong and permanent.
Dynamic Jahn-Teller distortion: In some molecules, the distortion is not seen either due to random movements of bonds which does not allow the measurement within a time frame or else the distortion is so weak as to be negligible. However the distortion can be seen by freezing the molecule at lower temperatures. This condition is referred to as dynamic Jahn-Teller distortion.
E.g.
1) The complexes of the type M2PbCu(NO2)6 show dynamic Jahn-Teller distortion.
Here, M= K, Rb, Cs, Tl;
They show tetragonal symmetry at lower temperatures due to static Jahn-Teller distortion. But at higher temperatures, these molecules appear octahedral due to the dynamic Jahn-Teller effect.
2) The complex [Fe(H2O)6]2+ shows dynamic Jahn-Teller distortion and appears octahedral. In this case, the distortion is small since the degeneracy occurs in t2g orbitals. Remember Fe2+ in above complex is a high spin d6 system with t2g4 eg2 configuration.
According to one school of thought, the complexes formed by low spin d8 systems, like Ni(II), are electronically degenerate in the octahedral environment since the strong field ligands around the metal ion force the two electrons in the eg orbitals to pair up. Hence they also undergo Jahn Teller distortion by completely eliminating the ligands on the z-axis to become square planar.
E.g. [Ni(CN)4]2- is a square planar complex.
The same arguments are also applicable to the square planar complexes formed by Pt, Pd etc.
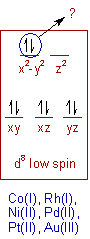
But this argument is debatable since the pairing of electrons is against the Hund’s rule.
According to another school of thought, the low spin d8 systems are not at all electronically degenerate in the octahedral environment. Therefore no question of Jahn-Teller distortion. They exhibit square planar geometry simply because the crystal field splitting energy, Δ in this geometry is very high since the ligands are of strong field. This will also increases the CFSE value.
The square planar geometry is thought to be resulted due to infinite distortion of octahedral geometry along the z-axis (see the diagram below). However this is not the Jahn-Teller distortion. Why? Because, the octahedral d8 is NOT electronically degenerate.
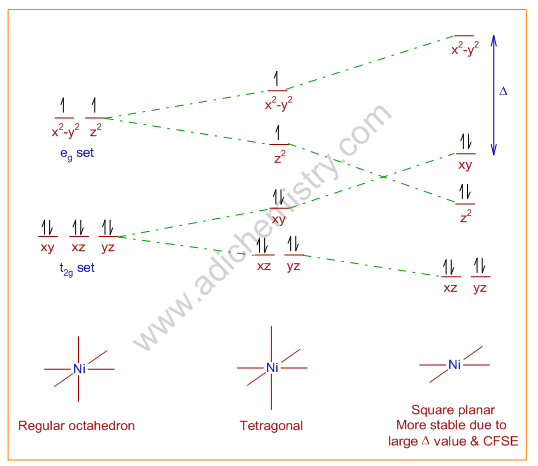
On the other hand, the high spin Ni(II) complexes, like NiCl42-, are tetrahedral. It is because the Δ value in presence of weak field ligands is low and does not favor the square planar geometry. Its geometry is tetrahedral because in this configuration, the ligands are placed as far away as possible from each other.
But all types of complexes of Pt, Pd; irrespective of whether they are high spin or low spin, are square planar.
The reasons are:
1) As we move down the group, the Δ value increases by about 50% in all cases.
2) Ligand replulsions are minimized due to large size of the metal. This favors square planar geometry.
3) Due to the π-interactions of d-orbitals of metals with the orbitals of ligands the stability of square planar geometry increases.
Note: However the π-interations are not possible in case of Ni(II) due to small size of its d-orbitals (no effective overlapping).
a) Tetragonal structure of Cu(II) complexes: The Cu(II) ion is a d9 system and expected to show Jahn-Teller distortion and depart considerably from octahedral geometry. The Cu(II) ion in the aqueous medium is surrounded by six water molecules in tetragonal geometry i.e., four of which are at the corners of square plane and are at shorter distances with stronger interactions, whereas, the remaining two are weakly interacting with the metal ion at distant axial positions.
b) Structure of hydrated copper(II) sulphate, CuSO4.5H2O and other Cu(II) complexes: In the solid CuSO4.5H2O, the copper ion is surrounded by four water molecules in square planar geometry. There are also weak interactions with the sulphate ions in the axial positions. The 5th water molecule is hydrogen bonded to the sulphate ion. That means the two water molecules on the axial positions are completely eliminated and substituted by sulphate ions while forming the solid.
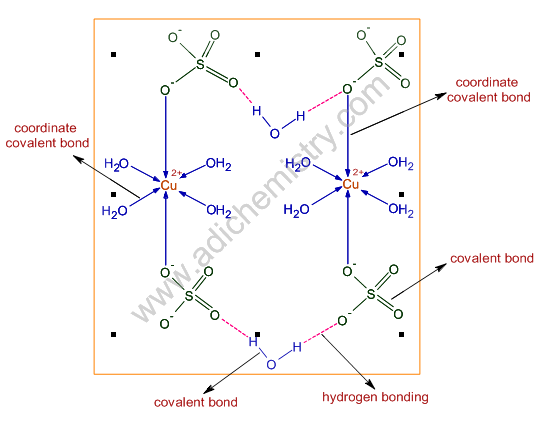
Note: Due to interactions with these ligands, the d orbitals are split into different energy levels, which makes d-d transitions possible. It absorbs red color and transmits blue color during the d-d transition. But upon heating, all the water molecules are lost, which makes all the d orbitals degenerate again. Hence the anhydrous CuSO4 is colorless.
c) Extra stability of Cu2+ ions: The relative stabilities of complexes formed by high spin divalent first row transition metal ions is given by Irving-Williams series. The stability order is shown below:
Mn(II) < Fe(II) < Co(II) < Ni(II) < Cu(II) > Zn(II)
The extra stability of Cu(II) ion can be explained by taking into account of Jahn-Teller distortion of this d9 ion.
d) Other examples: Because of Jahn-Teller distortion:
* In the crystalline KCuF3, the two Cu- F distances are at 1.96 A0 and the remaining four Cu - F distances are at 2.07 A0. It is a case of Z-compression.
* In [Cu(hfacac)2(bipy)], there are two short Cu-O bonds and two long Cu–O bonds. (where hfacac = hexafluoroacetylacetone anion; bipy = 2,2’-bipyridine). It is an example for Z-out distortion.
* Cu(II) cannot form [Cu(en)3]2+ since JT distortion brings strain into the ethylene diamine molecule that is added along z-axis. Hence only [Cu(en)2(H2O)2]2+ is formed.
E.g. The absorption band in the electronic spectrum of aqueous Ti(III), a d1 octahedral system, is not symmetric but rather shows a distinct broad shoulder. It is because of Jahn-Teller distortion.
The Jahn-Teller distortion is negligible in case of degenerate t2g orbitals in the ground state. Hence no distortion in the ground state. But when the electron gets excited, the configuration now becomes t2g0 eg1, which is again degenerate. Hence in the excited state, the Jahn Teller distortion is possible. Now the promotion of electron may occur to either of the two non degenerate eg orbitals, the dz2 and dx2-y2. Thus, two transitions are possible. But a shoulder appears since the energy difference between two transitions is small.
The [Cr(H2O)6]2+ undergoes substitution easily since the Cr(II) ion is a high spin d4 system with one electron in the eg orbital. Hence it is electronically degenerate and shows Jahn-Teller distortion. Hence the hydrated Cr(II) ion is coordinatively labile.
On the same lines, the easy substitution of [Co(NH3)6]2+ by water molecules can be explained. In this case the Co(II) ion is coordinatively labile since it is a low spin octahedral d7 ion which is degenerate in eg set. Hence it undergoes J-T distortion and is labile.
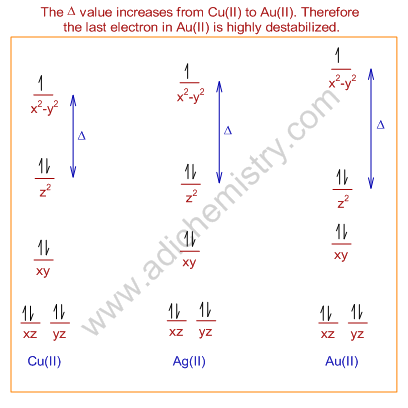
Au(II) ion is less stable and undergoes disproportionation to Au(I) and Au(III) even though the Cu(II) and Ag(II) ions are comparatively more stable. One may expect same stability since all are d9 systems and undergo the Jahn-Teller distortion.
However, the Δ value increase down the group. Hence, in Au(II) ion, it reaches a maximum, which causes high destabilization of the last electron, which is now occupying the dx2-y2. This makes Au(II) reactive, which may undergo either oxidation to Au(III), a d8 system or reduction to Au(I), a d10 system.
The d8 system, Au(III) is stable as the electron from the dx2-y2 is removed. Mostly it prefers square planar geometry and more stable than both Au(II) and Au(I). The d10 system, Au(I) favors mostly linear geometry with coordination number = 2.
Question-Why do the d9 systems usually not undergo complete distortion to square planar geometry?
Answer: Usually, the d9 systems are tetragonal with elongated bonds on z-axis and do not undergo complete distortion to square planar. It is because the last electron will be placed in highly destabilized dx2-y2 if they get square planar geometry. But the low spin d8 complexes may undergo complete distortion to square planar geometry.
Question-1: Which metal complex ion is expected to be subject to a Jahn-teller distortion?
A) Cu2+
B) Ni2+
C) Ca2+
D) Cr3+
Answer: A
Question-2: Which of the following does not show octahedral geometry,
1) [Cu(CN)4]2+
2) XeF4
3) [NiCl4]2-
4) All
Answer: 4
Question-3: Strong Jahn-teller distortion is not observed for octahedral complexes of:
1) Cu2+
2) Low spin Cr2+
3) High spin Mn3+
4) High spin Cr2+
Answer: 2
Question-4: Which of the following shows strong Jahn teller distortion?
1) Fe3+
2) High spin Co2+
3) Ti2+
4) Low spin Co2+
Answer: 4
Question-5: Jahn teller effect is not observed in high spin complexes of:
A) Mn2+
B) Cr2+
C) Cu2+
D) Fe3+
Answer: A
Question-6: Which metal complex ion is expected to be subject to a Jahn teller distortion?
1) Low spin Co2+
2) High spin Cr2+
3) Ti2+
4) All
Answer: 4
Question-7: Which of the following d-configuration shows strong distortion from octahedral geometry?
1) d1
2) d2
3) d9
4) None
Answer: 3
Question-8: Why does the absorption spectrum of aqueous [Ti(OH2)6]3+ exhibit a broad band with a shoulder?
1) Due to Jahn-Teller distortion in the ground state
2) Due to Compton effect
3) Due to jahn-Teller distortion in the excited state
4) Due to square planar geometry
Answer: 3