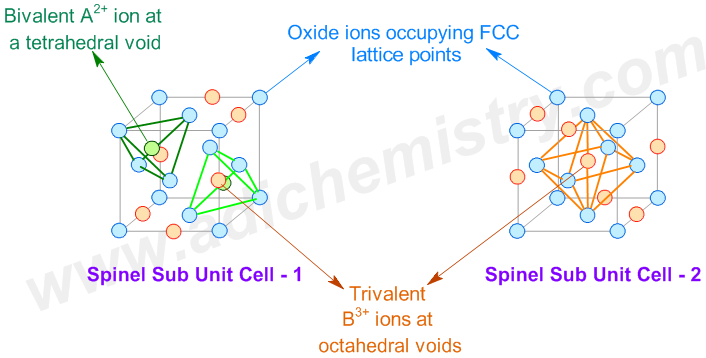
The spinels have the general chemical formula AB2X4.
Where:
AII = a divalent cation like Mg, Cr, Mn, Fe, Co, Ni, Cu, Zn, Cd, Sn
BIII = a trivalent cation like Al, Ga, In, Ti, V, Cr, Mn, Fe, Fe, Co, Ni
X = O, S, Se etc.
Examples of Normal Spinels: MgAl2O4 (known as spinel), Mn3O4, ZnFe2O4, FeCr2O4 (chromite) etc.
A spinel unit cell is made up of 8 FCC cells. The anions (usually oxide ions: O2-) occupy the FCC lattice points. The divalent AII cations occupy 1/8th of the tetrahedral voids, whereas the trivalent BIII cations occupy one half (1/2) of octahedral voids.
We know that in one FCC lattice unit cell, the effective number of atoms (or ions) occupying the lattice points is 4. At the same time, the effective number of tetrahedral voids (holes) = 8 and that of octahedral voids = 4.
That means, in a normal spinel,
The number of anions occupying the lattice points of 8 FCC unit cells = 8 x 4 = 32 .
Whereas, the number of divalent AII cations occupying 1/8th of tetrahedral voids = 8 x 1/8 x 8 = 8
and the number of trivalent BIII ions occupying the half of octahedral voids = 8 x 1/2 x 4 = 16.
i.e. The ratio of AII : BIII : O2- = 8 : 16 : 32 = 1:2:4 which confirms with the formula of normal spinels.
Thus a normal spinel can be represented as: (AII)tet(BIII)2octO4

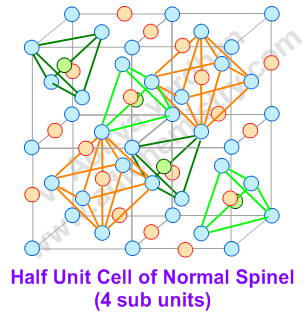
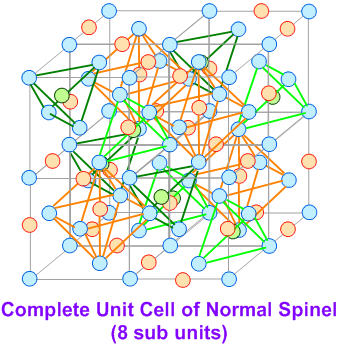
Now the question is "What are inverse spinels and the differences between the normal and inverse spinel structures?"
Structures of Inverse spinels (B(AB)O4): The AII ions occupy the 1/4th of octahedral voids, whereas one half of BIII ions occupy the 1/8th of tetrahedral voids and the other half occupy 1/4th of octahedral sites. It can be represented as: (BIII)tet(AIIBIII)octO4.
# anions occupying the lattice points of 8 FCC unit cells = 8 x 4 = 32 .
# divalent AII cations occupying 1/4th of octahedral voids = 8 x 1/4 x 4 = 8
# trivalent BIII ions occupying the 1/4th of octahedral voids = 8 x 1/4 x 4 = 8.
# trivalent BIII ions occupying the 1/8th of tetrahedral voids = 8 x 1/8 x 8 = 8.
i.e. The ratio of AII : BIII : O2- = 8 : (8+8) : 32 = 1:2:4 which confirms with the formula of inverse spinels.
Thus an inverse spinel can be represented as: (BIII)tet(AII)oct(BIII)octO4
Examples of Inverse spinels: Fe3O4 (ferrite), CoFe2O4, NiFe2O4 etc.
The above inverse spinels can also be written as:
Fe3O4 = FeIII(FeIIFeIII)O4
CoFe2O4 = FeIII(CoIIFeIII)O4
NiFe2O4 = FeIII(NiIIFeIII)O4
The number of octahedral sites occupied may be ordered or random. The random occupation leads to defected spinels.
E.g. NiAl2O4 for which the formula can be written as (Al0.75Ni0.25)tet [Ni0.75Al1.25]octaO4.
Another defected spinel is γ-Al2O3
| Spinel Type | AII ions | BIII ions |
| Normal | 1/8th Tetrahedral voids | 1/2 of Octahedral voids |
| Inverse | 1/4th Octahedral voids | 1/8th Tetrahedral voids 1/4th octahderal voids |
1) The relative sizes of A and B: In general, the smaller cation prefers to occupy the site of lower coordination i.e., tetrahedral site.
However, in the spinel, MgAl2O4 itself this factor is outweighed by greater lattice energy of smaller cation, Al3+, which occupies the octahedral site and thus by giving normal spinel structure. Otherwise the "spinel" will have the inverse spinel structure!
2) The Madelung constants for the normal and inverse structures: It is observed that the Madelung constants are same for both normal and inverse spinels and hence are not that much important in arriving at the type of spinels.
3) Ligand-Fleld Stabilization Energies: Applicable whenever there are transition metal ions and is discussed below.
The structures of spinels are affected by the relative LFSE values of metal ions. The ion with more LFSE value in octahedral geometry when compared to the LFSE in tetrahedral geometry tends to occupy octahedral sites.
The difference between the LFSE values in octahedral and tetrahedral geometries is referred to as Octahedral Site Stabilization Energy (OSSE).
“If the BIII ion has more CFSE gain in octahedral site than that of AII ion, a normal spinel structure is expected.”
“Whereas an inverse spinel is formed whenever the divalent AII ion has comparatively more CFSE gain in octahedral geometry than the trivalent BIII ion.”
* A normal spinel structure is assumed if both the divalent and the trivalent metals are non transition metals since no CFSE is involved.
* There is a tendency of formation of inverse spinel structure in some cases (not all the cases) which contain transition metal ions. This is because, the transition metal ion may get extra stability (LFSE) in octahedral geometry, prefers octahedral voids over tetrahedral ones.
* The d0; high spin d5, d10 ions have no preference between tetrahedral and octahedral coordination since the LFSE is zero.
* Usually d3 & d8 ions have strongest preference for octahedral geometry.
* Other ions with d1, d2, d4, d6, d7, d9 too have slightly more preference for octahedral symmetry.
* That means, if AII has d3 or d8 configuration and the BIII ion has configuration other than these, then the spinel is inverted.
* If the divalent AII is a transition metal (with configurations other than d0; highspin d5 & d10) and the BIII ion is a non transition metal, there is a tendency to form inverse spinel.
But there are exceptions like FeAl2O4 which has normal spinel structure.
* Above generalizations are valid for high spin systems as the oxide ion is expected to be a weak field ligand.
For example, Co3+ is a low spin system even in presence of oxo ligands due to high charge on the ion.
| AII | BIII | Structure |
|
Non transition metal |
Non transition metal | Spinel structure |
| Non transition metal or d0 or d5 or d10 transition metal |
A transition metal with
d1 or d2 or d3 or d4 or d6 or d7 or d8 or d9 configurations |
Spinel structure |
| A transition metal with
d1 or d2 or d3 or d4 or d6 or d7 or d8 or d9 configurations |
Non transition metal or transition meta with d0 or d5 or d10 configurations |
Inverse spinel |
| Transition metal with higher CFSE value | Transition metal with lower CFSE value | Inverse spinel |
1) MgAl2O4 has normal spinel structure since both the divalent and trivalent ions are non transition metal ions. There is no question of CFSE.
2) Mn3O4 is a normal spinel since the Mn2+ ion is a high spin d5 system with zero LFSE. Whereas, Mn3+ ion is a high spin d4 system with considerable LFSE.
3) Fe3O4 has an inverse spinel structure since the Fe(III) ion is a high spin d5 system with zero CFSE. Whereas the divalent Fe(II) is a high spin d6 system with more CFSE.
4) NiFe2O4 is again an inverse spinel since the divalent Ni2+ (a d8 ion) has more CFSE than the trivalent Fe3+ (a d5 ion).
5) FeCr2O4 is a normal spinel since the divalent Fe2+ is a high spin d6 ion with CFSE = 4 Dq and the trivalent Cr3+ is a high spin d3 ion with CFSE = 12 Dq. Hence Cr3+ gets more OSSE while occupying octahedral sites.
6) Co3O4 is a normal spinel. Even in the presence of weak field oxo ligands, the Co3+ is a low spin d6 ion with very high CFSE. It is due to high charge on Co3+. Hence all the Co3+ ions occupy the octahedral sites.
7) NiAl2O4 show random or defected inverse spinel. The CFSE of NiII is greater in octahedral than tetrahedral coordination. But Al3+ also has strong preference for octahedral sites due to high lattice energy. This leads to almost complete randomization of all the cations on all the available sites. Its formula can be written as (Al0.75Ni0.25)tet [Ni0.75Al1.25]octaO4.
The spinels can be ferromagnetic or anti ferrimagnetic depending on the structure and nature of metal ions. The unpaired spins of metal ions are coupled through shared oxide ions by super exchange process. In ferrite spinels, the spins of electrons at tetrahedral sites have one orientation, whereas the spins of electrons at octahedral sites have opposite orientation. If the number of spins in these two types of sites is equal, then that spinel will be antiferromagnetic. Otherwise, it will be ferromagnetic.
E.g. The inverse spinels - Fe3O4, NiFe2O4 and CoFe2O4 are ferrimagnetic. In these cases, the spins of trivalent ions are cancelled out since half of them belong to tetrahedral sites and the other half belong to octahedral sites. However, the spins of divalent ions are not cancelled. Hence they show ferrimagnetism.
In case of FeCr2O4 - a normal spinel, the number of spins of high spin Cr3+ (d3) ions is equal to the number of spins of high spin Fe2+ (d6) ions. Hence it is antiferromagnetic.
MgAl2O4 is diamagnetic since all the electrons in the metal ions are paired up.
Note: Antiferro magnetic substances show weak magnetism, whereas diamagnetic substances show no magnetism at all.
Question-1: Total number of octahedral voids per unit cell of AB2O4 spinel ferrite occupied by cations is:
A) 16
B) 8
C) 32
D) 4
Answer: A
Question-2: Which of the following adopts normal spinel structure?
1) Fe3O4
2) FeCr2O4
3) CoFe2O4
4) NiFe2O4
Answer: 2
Question-3: In normal spinel structure, MgAl2O4, the percentage of tetrahedral voids occupied is:
A) 25%
B) 100%
C) 8%
D) 12.5%
Answer: D
Question-4: O-2:CCP ; B+3:half of octahedral voids ; A+2:1/8 of tetrahedral voids, the space lattice described refers to:
1) Perovskite
2) Inverse spinel
3) Normal spinel
4) Rocksalt
Answer: 3
Question-5: In a spinel like structure Mg2+ is present at one of the tetrahedral void, Al3+ is present at half of octahedral voids, whereas FCC is formed by the O2-. Select the correct statement(s).
1) The formula of spinel is AlMg2O8
2) It is an inverse spinel
3) The formula of spinel is MgAl2O4
4) It is a mixed spinel
Answer: 3
Question-6: In a spinel structure, AB2O4 the divalent cations A2+ occupy x% of the tetrahedral voids, while B3+ occupy y% of the octahedral voids and z% of the tetrahedral voids. Then the value of (2(y-x+z)+25)/(100) is:
A) 0.25
B) 1
C) 0.75
D) 0.5
Answer: B
Question-7: In the normal spinel structure all the tri positive ions occupy,
A) Tetrahedral voids
B) FCC lattice points
C) Trigonal voids
D) Octahedral voids
Answer: D