Collision theory of rates of reactions was first proposed independently by Max Trautzb and William Lewis to explain the rates of bimolecular reactions occurring in gaseous state. The main postulates of this theory are:
1) Chemical reactions can occur only upon collisions between reactant molecules.
2) However all the collisions do not lead to the formation of products. Otherwise all the reactions could occur within a fraction of second since there are millions of collisions possible.
3) Only those collisions taking place between molecules in proper orientation and possessing certain minimum amount of energy can lead to the formation of products.
The minimum amount of energy required by the colliding molecules to yield the products is called Threshold Energy (ET).
The reactant molecules must cross this energy barrier to be converted to products.
4) The energy possessed by the normal reactant molecules under STP conditions is called 'Average Energy' .
The difference between threshold energy and average energy of the reacting molecules is called Activation energy (Ea).
Ea = Threshold energy (ET) - Average energy (ER)
5) Some molecules will get energy equal to or greater than the threshold energy during collisions and are called as activated molecules. These are denoted by asterisk(*).
6) The collisions taking place between activated molecules are called activated collisions (or) effective collisions (or) fruitful collisions. The products are formed only during the activated collisions.
A + A ---------> A* + A (normal collision; no product is formed)
A* + A* ---------> products (effective collision)
Where
A = normal molecule
A* = Activated molecule
Activated molecules constitute a small fraction of total molecules. Therefore the effective collisions constitute a small fraction of total collisions. Hence all the chemical reactions do not occur in a fraction of a second.
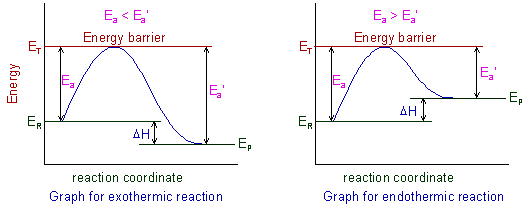
The concept of activation energies for both forward and backward reactions (Ea and Ea') can be shown graphically as:

Where
ER = Energy of reactants
EP = Energy of products
ET = Threshold energy
Ea = Activation energy of forward reaction
Ea' = Activation energy of backward reaction
ΔH = Enthalpy of reaction
The activation energy for forward reaction (Ea) is less than that of backward reaction (Ea') for exothermic reactions i.e., (Ea< Ea'). Whereas for endothermic reactions it is quite opposite i.e., (Ea> Ea').
The activation energy depends on the nature of chemical bonds, which are breaking during the reaction. Stronger the bonds, greater is the activation energy. However it does not depend on the enthalpy of the reaction.
7) The number of binary collisions per unit time, Z for a reaction involving gaseous reactants, A & B is given by:
![]()
Where
σAB= Collision diameter
μ= reduced mass
nA & nB are the number of molecules of A & B in unit volume
The value of collision frequency is very high of the order of 1025 to 1028 in case of binary collisions of gaseous molecules.
It is evident from the above equation that the number of collisions increases with increase in the average velocity, concentration and temperature of gaseous molecules. Also note that greater the collision diameter, greater is the number of collisions per unit time.
i.e.,
Z ∝ average velocity
Z ∝ number density of molecules
Z ∝ √T
Z ∝ σAB2
The fraction of effective collisions increases with increase in the total number of collisions. Hence the rate of a reaction is directly proportional to the collision frequency.
i.e., rate of reaction ∝ collision frequency (Z)
8) The relation between specific rate (k), temperature (T) and activation energy (Ea) can be given by Arrhenius equation as follows:
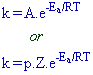
Where
k = specific rate (or) rate constant
A = pZ = Frequency factor
p = probability factor or steric factor or orientation factor
Z = no. of binary collisions per unit time
Ea = Activation energy
R = Universal Gas constant
T = Absolute Temperature
It is clear that the rate of a reaction is proportional to the temperature but inversely proportional to the activation energy.
The probability factor is related to the orientation of the molecules. It is necessary for colliding molecules to be properly oriented in space to give products. For simple and smaller molecules, the probability factor is higher than that for complex and bigger molecules. This is because the number of proper orientations is greater in case of simpler and smaller molecules (more explanation is given in the later sections)