ORBITAL ANGULAR MOMENTUM FORMULA
mvr = nh/2π
SOLVED PROBLEMS - IIT JEE - NEET

According to Bohr’s theory, the angular momentum of an electron in 5th orbit is:

(JEE MAIN 2006)

a) 25h/π 

b) 1.0h/π 

c) 10h/π

d) 2.5h/π

Logic:

The angular momentum (mvr) of electron in nth orbit is equal to nh/2π.

Solution:

For the electron in 5th orbit,

angular momentum = mvr = 5h/2π = 2.5h/π

Conclusion:

Correct option is "d".

Extra information

Note: nh/2π gives angular momentum of electron revolving in a circular orbit as proposed by Neils Bohr. However, the exact orbital angular momentum of electron in a given orbital is calculated by using the following equation. 

Related questions

1) The orbital angular momentum of an electron in 2s orbital is: 

(IIT JEE-1996) 

a) 0.5h/π 

b) 0 

c) h/2π

d) √2h/π 

Solution:

For s orbital, l = 0.

Therefore:

orbital angular momentum = 0.

2) For a d-electron, the orbital angular momentum is :

 (IIT JEE - 1997)

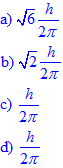
Solution:

Since for a d-electron, l = 2,

3) According to Bohr’s theory, which one of the following values of angular momentum of hydrogen atom is not permitted ?

 (EAMCET 2011-Medical)

a) 0.5h/π 

b) 1.25h/π 

c) h/π

d) 1.5h/π

Theory:

Bohr's atomic model is based on quantum theory, according to which, only definite values of angular momentum are possible for electron revolving in a circular orbit. It is given by mvr = nh/2π.

The principal quantum number, n can have only integral values i.e., 1, 2, 3, 4............

Solution:

Conclusion:

Answer to the question  is "b".

4) The angular momentum of an electron present in the excited state of hydrogen is 1.5h/π . The electron is present in:

 (EAMCET 2006-Medical)

a) Third orbit 

b) Second orbit 

c) Fourth orbit 

d) Fifth orbit

Solution:

1.5h/π = 3 x h/2π

Therefore n = 3 and the electron is in the third orbit of excited state.

5) In a hydrogen atom, the electron is at a distance of 4.768 Å from the nucleus. The angular momentum of the electron is:

 (EAMCET 2010-M)

a) 3h/2π 

b) h/2π 

c) h/π

d) 2h/π

Logic:

First find out the n value for the orbital using equation:

Then calculate the angular momentum using the formula:

mvr =  nh/2π 

Solution:

Radius of orbit (r) = 0.529 x n²/Z  Å

or

4.768 Å = 0.529 x n²/1  Å

or

n² = 4.768 / 0.529 = 9.013

Therefore,

n = 3

And the angular momentum, mvr = 3h/2π

6) In a many-electron atom, the total orbital angular momentum (L) and spin (S) are good quantum numbers instead of the individual orbital (l₁, l₂) and spin (s₁, s₂) angular momenta in the presence of

 (CSIR UGC NET DECEMBER 2012)

1) inter-electron repulsion

2) spin-orbit interaction

3) hyperfine coupling

4) external magnetic field.

Explanation:

The strong inter electron repulsion in many electron atoms results in coupling of individual orbital angular momenta and spin angular momenta. Therefore the total orbital angular momentum (L) and total spin angular momentum (S) are good quantum numbers instead of individual values.

7) For Hydrogen-like species, the incorrect statement is:

A) The energy of the bound electron is determined by spin quantum number, s.

B) The azimuthal quantum number ‘l’ specifies the magnitude of orbital angular momentum of electron.

C) Energy of the electron is determined by 'l'.

D) Every orbital has same angular momentum. 

Answer: B

8) For a hydrogen atom in an n = 4 state, the maximum possible z-component of orbital angular momentum is

 (BANARUS HINDU UNIVERSITY BHU MSC 2011)

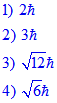
Explanation:

For n = 4, the possible 'l' values are 0, 1, 2 & 3.

The z-component of L is given by,

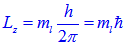
For maximum possible 'l' value i.e 3 and for this m_l can have values -3, -2, -1, 0, +1, +2, +3.

Substitute the maximum m_l value to get the answer.

Answer: 2

Orbital angular momentum - Homework - Practice questions

1) What are the orbital angular momentum values of electrons in 2p and 3p orbitals in hydrogen atom?

2) What is the difference between angular momentum values of ground and 1st excited states of hydrogen atom?

3) What is the angular momentum of electron in 3d orbital?

Jump to Relation between Energy & Wavelength of photon - IIT JEE - NEET - IT JAM solved problems