ATOMIC STRUCTURE
The early theories describing the atomic structure are based on classical physics. However these theories could not explain the behavior of atom completely. The modern view of atomic structure is based on quantum theory introduced by Max Planck.
Before learning the quantum theory, it is necessary to understand the nature of light.
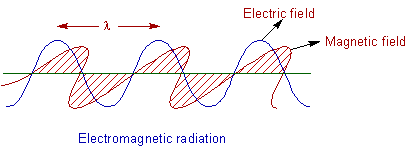
Light is considered as an electromagnetic radiation. It consists of two components i.e., the electric component and the magnetic component which oscillate perpendicular to each other as well as to the direction of path of radiation.
The electromagnetic radiations are produced by the vibrations of a charged particle. The properties of light can be explained by considering it as either wave or particle as follows (dual nature).
According to the wave theory proposed by Christiaan Huygens, light is considered to be emitted as a series of waves in all directions. The following properties can be defined for light by considering the wave nature.
Wavelength (λ): The distance between two successive similar points on a wave is called as wavelength. It is denoted by λ.
Units: cm, Angstroms (Ao), nano meters (nm), milli microns (mµ) etc.,
Note:
1 Ao = 10-8 cm.
1 nm= 10-9m = 10-7cm
Frequency (ν): The number of vibrations done by a particle in unit time is called frequency. It is denoted by 'ν'.
Units: cycles per second = Hertz = sec-1.
Velocity (c): Velocity is defined as the distance covered by the wave in unit time. It is denoted by 'c'.
Velocity of light = c = 3.0 x 108 m.sec-1 = 3.0 x 1010 cm.sec-1
Note: For all types of electromagnetic radiations, the velocity is a constant value. The relation between velocity (c), wavelength (λ) and frequency (ν) can be given by following equation.
velocity = frequency x wavelength
c = νλ
Wave number (
): The number of
waves spread in a length of one centimeter is called wave number. It is denoted
by . It is
the reciprocal of wavelength, λ.
units: cm-1, m-1
Amplitude: The distance from the midline to the peak or the trough is called amplitude of the wave. It is usually denoted by 'A' (a variable). Amplitude is a measure of the intensity or brightness of light radiation.
Though most of the properties of light can be understood by considering it as a wave, some of the properties of light can only be explained by using particle (corpuscular) nature of it. Newton considered light to possess particle nature. In the year 1900, in order to explain black body radiations, Max Planck proposed Quantum theory by considering light to possess particle nature.
Black body: The object which absorbs and emits the radiation of energy completely is called a black body. Practically it is not possible to construct a perfect black body. But a hollow metallic sphere coated inside with platinum black with a small aperture in its wall can act as a near black body. When the black body is heated to high temperatures, it emits radiations of different wavelengths.
The following curves are obtained when the intensity of radiations are plotted against the wavelengths, at different temperatures.
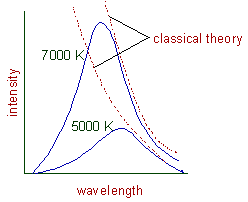
Following are the conclusions that can be drawn from above graphs.
1) At a given temperature, the intensity of radiation increases with wavelength and reaches a maximum value and then starts decreasing.
2) With increase in temperature, the wavelength of maximum intensity (λmax) shifts towards lower wavelengths. According to classical physics, energy should be emitted continuously and the intensity should increase with increase in temperature. The curves should be as shown by dotted line.
In order to explain above experimental observations Max Planck proposed the following theory.
Quantum theory:
1) Energy is emitted due to vibrations of charged particles in the black body.
2) The radiation of energy is emitted or absorbed discontinuously in the form of small discrete energy packets called quanta.
3) Each quantum is associated with definite amount of energy which is given by the equation E=hν.
Where
h = planck's constant = 6.625 x 10-34 J sec = 6.625 x10-27 erg sec
ν= frequency of radiation
4) The total energy of radiation is quantized i.e., the total energy is an integral multiple of hν. It can only have the values of 1 hν or 2 hν or 3 hν. It cannot be the fractional multiple of hν.
5) Energy is emitted and absorbed in the form of quanta but propagated in the form of waves.
Einstein generalized the quantum theory by applying it to all types of electromagnetic radiations. He explained photoelectric effect using this theory.
Photoelectric Effect: The ejection of electrons from the surface of a metal, when the metal is exposed to light of certain minimum frequency, is called photoelectric effect.
The frequency of light should be equal or greater than a certain minimum value characteristic of the metal. This is called threshold frequency, νo.
The photoelectric effect cannot be explained by considering the light as wave. Einstein explained photoelectric effect by applying quantum theory as follows:
1. All electromagnetic radiations consists of small discrete energy packets called photons. These photons are associated with definite amount of energy given by the equation E=hν.
2. Energy is emitted, absorbed as well as propagated in the form of photons only.
3. The electron is ejected from the metal, only when a photon of sufficient energy strikes the electron. When a photon strikes the electron, some part of the energy of photon is used to free the electron from the attractive forces in the metal atom and the remaining part is converted into kinetic energy.
hν = W + K.E
Where
W = energy required to overcome the attractions
K.E = kinetic energy of the electron
Since the frequency corresponding to the minimum energy required to overcome the attraction is called threshold frequency, νo, the above equation can be written as:
hν = hνo + K.E
or
K.E = hνo- hν = h(νo- ν)
Author: Aditya vardhan Vutturi