Electrochemistry deals with the study of electrochemical processes and their applications which involve:
i) the conversion of electrical energy into chemical energy and
ii) the conversion of chemical energy into electrical energy.
It is possible to carry out a non spontaneous chemical reaction by applying sufficient electrical voltage in an electrochemical cell. In this case, the electrical energy is converted to chemical energy.
E.g. Preparation of sodium metal by Down's process.
It is also possible to produce electrical energy by carrying out a spontaneous chemical reaction in a suitable device called galvanic cell or voltaic cell.
E.g. Batteries and fuel cells.
Electrochemistry is an interdisciplinary subject. Its scope and practical applications covers several fields of science including metallurgical processes, biological sciences, analytical techniques, space research, energy systems etc.
Electricity: The term electricity refers to a form of energy or variety of phenomenon resulting from the accumulation of static charges or flow of charged particles.
Electric charge: The electric charge is the fundamental and conserved property of some subatomic particles which determines their electromagnetic interactions. It exhibits two states i.e., positive and negative.
In SI units, the electric charge is measured in Coulombs (C).
The smallest value of “free” charge known in nature is the charge of an electron or a proton, which has a magnitude of 1.602 x 10-19 Coulomb.
The charge on one electron is: -1.602 x 10-19 C.
Whereas the charge on a proton is equal to: +1.602 x 10-19 C.
Electric field: It is an influence produced by an electric charge on other charges in its vicinity.
A charged particle experiences force when placed in an electric field. The electric field exerts a force on charged particles, accelerating them in the direction of the force, in either the same or the opposite direction of the electric field.
Hence some amount of work has to be done against this force to bring the charged particle to a certain point in an electric field.
Electric potential: The electric potential at any point in an electric field is defined as the energy required to bring a unit charge from an infinite distance to that point.
It is usually measured in volts (V). Volt can be formally defined as the ratio of energy in joules to the charge in coulombs.
The absolute electric potential cannot be measured. However, the difference in electric potential between two points can be measured and has more practical usage.
Electric potential difference or voltage: It is the energy required to move a unit charge between two specified points in an electric field. However, it is usually referred to as electric potential or some times as voltage.
![]()
One Volt (V) is equal to 1 Joule per 1 Coulomb.
![]()
Electromotive force (emf): Formally it is same as electric potential difference. It is the potential energy divided by electric charge and is measured in volts.
It can be defined as the external work expended per unit of charge to produce an electric potential difference thereby causing the current to flow in the circuit.
Note: Though there are several different definitions given across the literature, the above explanation is sufficient in electrochemistry.
Current: Formally it is the flow of charged particles like electrons, protons, ions. The strength of current (I) is defined as the charge transferred in unit time. It is measured in amperes (A).
![]()
One ampere (A) is defined as 1 coulomb of electricity transferred in one second.
![]()
Resistance (R): The tendency of a material to stop the flow of current is known as resistance. It is measured in ohms (Ω).
According to Ohm's law, the resistance offered by a substance is directly proportional to its length (l), but inversely proportional to its cross sectional area (A).
![]()
In case of electrolytic solutions, 'l' represents the distance between two electrodes and the 'A' is the cross sectional area of the electrodes.
The above equation can also be written as:
![]() -------- equation (1)
-------- equation (1)
Where ρ is the proportionality constant and is known as specific resistance or resistivity.
If A = 1 cm2 and l = 1 cm, then R = ρ.
Therefore, the specific resistance can be defined as follows:
Specific resistance or resistivity (ρ): It is the resistance offered by a material or solution occupying one cm3 volume.
It is measured in:
ohm. cm (in C.G.S system)
or
ohm. m (in S.I system)
Its unit can be derived as follows:
![]()
Conductance (G): It is the tendency of a material to allow the flow of current through it. It is the reciprocal of resistance.
It is measured in ohm-1 = mho = Siemens.
![]()
By substituting, R from equation (1):
![]() ---------- equation (2)
---------- equation (2)
Where
![]()
From the equation (2),
![]()
If A = 1 cm2 and l = 1 cm, then κ = G.
Therefore the specific conductance can be defined as:
specific conductance or conductivity (κ): It is the conductance of a material or solution between two electrodes of cross sectional area 1 cm2 and separated by 1 cm distance.
Note that above solution is occupying one cm3 volume.
It is measured in:
ohm-1. cm-1 = mho. cm-1 (C.G.S system)
or
Siemens. m-1 (S.I system)
* The specific conductance depends on the nature of substance or the electrolyte.
* It increases with increase in concentration of the electrolytic solution since the number of ions per unit area increases.
Cell constant (G*): The ratio of the distance between the electrodes, l to the cross sectional area, A of the electrodes is known as cell constant.
![]()
The cell constant can be determined by using following relations which can be derived easily from expressions discussed above.
![]()
Based on electrical conductivity, the materials are divided into two types as follows:
1) Insulators: The substances which resist the flow of electric current through them are called insulators. They do not have free electrons or freely moving charged particles.
E.g. Organic polymers (like plastics), glass, diamond, quartz etc.,
2) Conductors: The substances which allow the flow of electricity through them with little resistance are known as conductors.
They are again divided into:
i) Metallic or electronic conductors: The conductors which conduct the electricity through the electrons.
E.g. All metals, Graphite etc.
In case of metallic conductors;
* No chemical reaction occurs during the conduction of electricity.
* Conductivity decreases with increase in temperature due to vibrational disturbances.
ii) Electrolytes: The substances which furnish oppositely charged ions for the conduction of electricity.
E.g :- NaCl, KCl, CH3COOH, HCl etc.
In case of electrolytes;
* There is flow of ions towards the oppositely charged electrodes.
* During conduction of electricity through electrolytes, oxidation occurs at anode whereas reduction occurs at cathode i.e., a chemical reaction occurs.
* The conductivity increases with increase in temperature as the extent of ionization increases.
The electrolytes undergo dissociation to furnish ions either in molten state or in aqueous solutions. Depending on the extent of ionization (or dissociation) in water, the electrolytes are further divided into:
a) Strong electrolytes: Undergo complete ionization in water.
E.g. NaCl, KCl, K2SO4, HCl, H2SO4,NaOH, NaNO3 etc.
b) Weak electrolytes: Under go partial ionization in water.
E.g. HF, CH3COOH, NH4OH, HCOOH etc.
Non-electrolytes: The substances which do not furnish ions for electrical conduction are called non-electrolytes.
E.g : urea, glucose, sucrose etc.
Equivalent conductivity (Λ): The conductance of that volume of solution containing one equivalent of an electrolyte is known as equivalent conductivity. It is denoted by Λ.
Let us consider the V cm3 of solution containing one equivalent of an electrolyte. Its conductance is equal to equivalent conductance, Λ.
Also we know that the conductance shown by 1 cm3 solution (between two electrodes of cross sectional area 1 cm2 and separated by a distance of 1 cm) containing this electrolyte is called specific conductance, κ.
i.e.,
the conductance of V cm3 --------- Λ
the conductance of 1 cm3 --------- κ
Therefore:
Λ = κ.V ---------- equation (3)
We know that the normality (N) of a solution is given by the equation:
![]()
For above electrolytic solution, no. of equivalents, ne = 1.
Hence
![]()
By substituting the above value in the equation (3), we can now write:
![]()
Units of Λ:
![]()
= cm2 . ohm-1. equiv-1 = cm2 . mho. equiv-1
or
m2 . Siemens. equiv-1
Molar conductivity (Λm or μ): The conductance of that volume of solution containing one mole of an electrolyte is known as molar conductivity. It is denoted by Λm or μ.
It is related to specific conductance, κ as:
μ = κ.V
or
![]()
Where
M = molarity of the electrolytic solution.
Units of μ:
= cm2 . ohm-1. mol-1 = cm2 . mho. mol-1
or
m2 . Siemens. mol-1
The relation between equivalent conductance, Λ and molar conductance, μ can be given by:
μ = Λ x equivalent factor of the electrolyte
The equivalent factor of the electrolyte is usually the total charge on either anions or cations present in one formula unit of it. It may be equal to basicity in case of acids or equal to acidity in case of bases.
THE FACTORS AFFECTING THE CONDUCTANCE OF ELECTROLYTE SOLUTIONS
Temperature: The conductance of an electrolyte solution increases with increase in the temperature due to increase in the extent of inonization.
Nature of electrolyte:
* The strong electrolytes undergo complete ionization and hence show higher conductivities since they furnish more number of ions.
* Whereas weak electrolytes undergo partial ionization and hence show comparatively low conductivities in their solutions.
Ionic size & mobility:
* The ionic mobility decreases with increase in its size and hence conductivity also decreases.
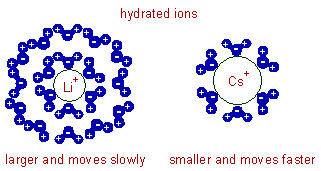
E.g. In molten state, the conductivities of lithium salts are greater than those of cesium salts since the size of Li+ ion is smaller than that of Cs+ ion.

* However, in aqueous solutions the extent of hydration affects the mobility of the ion, which in turn affect the conductivity. Heavily hydrated ions show low conductance values due to larger size.
E.g. In aqueous solutions Li+ ion with high charge density is heavily hydrated than Cs+ ion with low charge density. Hence hydrated Li+ bigger than hydrated Cs+ . As a result, lithium salts show lower conductivities compared to those of cesium salts in water.
The nature of solvent and its viscosity:
* The ionic mobility is reduced in more viscous solvents. Hence the conductivity decreases.
Concentration:
* The specific conductance (κ) increases with increase in concentration of solution as the number of ions per unit volume increases.
* Whereas, both the equivalent conductivity and molar conductance increase with decrease in concentration (i.e. upon dilution) since the extent of ionization increases.
Explanation: Since the concentration decreases, one can expect decrease in equivalent conductivity due to decrease in available number of ions per unit volume. However the increase in volume (V) factor more than compensates this effect. The volume must be increased in order to get one equivalent of electrolyte since the concentration is decreased. Hence the net effect is increase in equivalent conductivity.
Limiting equivalent conductivity (Λo):
The equivalent conductivity reaches a maximum value at certain dilution and does not change upon further dilution (i.e., by adding solvent further). This concentration is also termed as infinite dilution.
The equivalent conductivity at infinite dilution is known as the limiting equivalent conductivity (Λo). At this dilution, the ionization of even the weak electrolyte is complete.
However at infinite dilution (i.e., when concentration approaches zero) the conductivity of the solution is so low that it cannot be measured accurately. Therefore the limiting equivalent conductivity of an electrolyte is calculated by using Debye-Huckel-Onsagar equation as explained below.
Conductance ratio (α) : The ratio of the equivalent conductance at given concentration, Λc to that at infinite dilution, Λo is called conductance ratio, α.
![]()
For weak electrolytes, the 'α' is also called as degree of ionization.
It is possible to determine the equivalent conductivities of electrolytes in water at given concentration by using Debye-Huckel-Onsagar equation.
![]()
Where
Λc= equivalent conductivity at given concentration.
Λo= equivalent conductivity at infinite dilution.
c = concentration
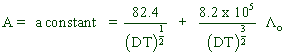
D = Dipole moment of water
T = Absolute temperature
A straight line with negative slope is obtained when the equivalent conductivity values (Λc) of strong electrolytes are plotted against square roots of different concentrations (√c). The equivalent conductivity at infinite dilution (Λo) can be determined by extending this straight line to zero concentration.
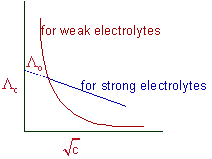
However the equivalent conductivity of weak electrolytes increases steeply at very low concentrations (see the above graph) and hence their limiting values (Λo) cannot be determined by extrapolating the Λc to zero concentration.
Therefore, Λo for weak electrolytes is obtained by using Kohlrausch law of independent migration of ions, which is described in the next section.
Author: Aditya vardhan Vutturi