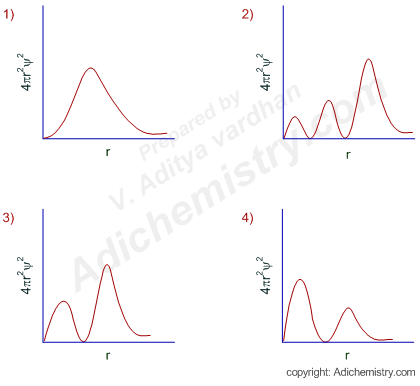
Logic:
Radial distribution curve gives an idea about the electron density at a radial distance from the nucleus. The value of 4πr2ψ2 (radial probability density function) becomes zero at a nodal point, also known as a radial node.
The number of radial nodes for an orbital = n-l-1.
Where n = principal quantum number and l= azimuthal quantum number.
Since n = 3 and l = 1 for the given atomic orbital (3p orbital), the number of radial nodes = 3-1-1 = 1.
Hence the radial probability distribution curve should contain a trough representing a radial node.
There are two graphs showing this behavior. The correct one is option-3 since the position of principal maximum (largest peak) occurs at a greater distance. I mean the crest with greater height should be farther away from the nucleus when compared to the smaller crest.
The amplitude or intensity of three-dimensional electron wave is known as Wavefunction and is represented by ψnlm (r,θ, Φ). It has both radial and angular parts.
ψnlm (r,θ, Φ) = Radial part x Angular part = Rnl(r) x Φlm(θ, Φ)
where,
Rnl(r) = Radial wavefunction
Φlm(θ, Φ) = Angular wavefunction
The square of the radial wavefunction is known as radial probability density.
Radial probability density = R2nl(r)
It is the probability of finding the electron within the spherical shell enclosed between a sphere of radius 'r + dr' and a sphere of radius "r' from the nucleus.
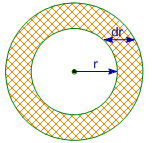
The relation between radial probability and radial probability density is given as:
Radial Probability = Radial Probability Density x Volume of spherical shell = 4πr2drR2nl(r)
It is also known as radial probability density function, it is given by 4πr2R2nl(r). In the graphs shown in question, ψ2 is shown instead of R2nl(r). It gives idea about the distribution of electron density at a radial distance around the nucleus without considering the direction or angle.
Q-1: Which of the following statements is/are correct?
1) The radial probability distribution curves for 2s atomic orbital has one trough representing a radial node.
2) The radial probability distribution curves for 2s, 3p and 4d atomic orbitals are similar in shape (source: http://www.adichemistry.com)
3) The number of angular nodes cannot be found using radial distribution curves.
4) All
Answer: 4
All the statements are correct.
* The number of radial nodes for 2s orbital = n-l-1 = 2-0-1 = 1.
* Since 2s, 3p and 4d orbitals have the same number of radial nodes, the radial distribution curves have similar shapes. However, the principal maxima are at different radial distances from the nucleus.
* Angular nodes or nodal planes have directional nature and hence angular part of the wavefunction should be employed to get information about them. The radial distribution curves have no clue about angular nodes.
Q-2: Which of the following atomic orbital with 1 angular node shows 3 maxima in its radial probability distribution curve?
1) 3s
2) 5d
3) 4p
4) None of the above
Answer: 3
Since there are 3 maxima, the number of radial nodes must be 2. The 3s, 5d and 4p orbitals have two radial nodes. However, only the p orbitals have one angular node.
Q-3: The radial probability distribution curve obtained for an orbital wavefunction of valence electron of an alkaline earth metal atom has 4 peaks. The metal is:
1) Potassium
2) Calcium
3) Barium
4) Magnesium
Answer: 2
Since there are 3 peaks, the number of radial nodes is 3. Hence the valence electron of alkaline earth metal atom resides in 4s orbital. Therefore the metal is Calcium.
Q-4: The number of peaks observed in the radial distribution curve for 4p atomic orbital is:
A) 1
B) 2
C) 3
D) 0
Answer: C
The number of radial nodes in 4p orbital = n-l-1 = 4-1-1 = 2
Therefore, the number of peaks = 3.
Question 1) Is it possible to get the shapes of orbitals with the help of radial probability distribution curves?
Answer: No. Since radial probability distribution curves are plotted for electron density at radial distance for a spherical shell, there is no direction or angle is mentioned. Hence it is not possible to get the exact shape of atomic orbitals from radial distribution curves. We have to take the support of angular distribution curves.
Question 2) What is exactly a radial node? (copied from adichemistry.com). What is the difference between an angular node and a radial node?
Answer: Radial nodes are regions around the nucleus where the probability of finding electron is zero. They do not pass through the nucleus. The angular nodes are the planes where the probability of finding electron is zero and they pass through the nucleus.
Question 3) Calculate the number of radial nodes for 1s, 2s, 3s, 2p, 3p, 4p, 3d, 4d & 5d orbitals.
Hint: Use the equation n-l-1.
Question 4) How many radial nodes are there in 4f orbital?
Answer: number of radial nodes = n-l-1 = 4 - 3 - 1 = 0 radial nodes for 4f orbital.
Question 5) At what distance is the radial probability maximum for 1s orbital?
Answer: 0.053 nm. It is equal to the Bohr's radius of 1st orbit in hydrogen atom.
Question 6) Radial probability distribution curves are the plots of 4πr2ψ2 vs distance from the nucleus. The curve has number of maxima which is different for different orbitals. The number of spherical nodes present in 4p orbital and 5d orbital respectively are,................. (Answer: 2 & 2)
Question 7) The variation of radial probability density R2 (r) as a function of distance r of the electron from the nucleus for 3p orbital, when shown graphically, the graph shows .......... peaks with the smallest one ......... to the nucleus. (Answer: 2, closer)
Question 8) The radial probability distribution function for a hydrogen atom state has one peak, at r = 0.476 nm. The nl spectroscopic notation of this state is......? (solved - free)
A) 3p
B) 3d
C) 4f
D) 2p
Answer: radius of nth orbit (r) = 0.053 x n2 nm
Plugin the values now, 0.476 = 0.053 x n2 nm
or n = 3
Since the graph has only one peak, there is no nodal region. This is possible for 3d orbital.
Question 9) The probability distribution curve for 2s electron appears like that of:
1) 1s orbital
2) 2p orbital
3) 3p orbital
4) 3d orbital
Answer: 3
10) Draw the graph of radius of orbit in hydrogen atom as a function of orbit number.
11) What is the value of (n + l + r) in a given wave function, where n = principle quantum number and l = azimuthal quantum number and r = total number of node present in given wave function =181(6π)1/2(Za)7/2r2e−Zt/3a(3cos2θ−1)
12) The radial probability curve obtained for an orbital wave function has 3 peaks and 2 radial nodes. The valence electron of which one of the following metals does this wave function correspond to:
A) Ca
B) Mg
C) Li
D) Cs
Answer: B
Question 13) The radial probability distribution curve of an orbital of H (hydrogen atom) has 4 local maxima. If orbital has 3 angular nodes then orbital will be......?
Solution:
The 4 local maxima indicate 3 radial nodes.
The 3 angular nodes denote an 'f' orbital with azimuthal quantum no (l) = 3.
No. of radial nodes = n - l - 1 = 3
Therefore, n = 3 + 3 +1 = 7
Answer: The orbital is 7f.
Question 14) select the correct statement from the below given options.
A) number of peaks in radial probability distribution function versus radius is same as in probability density versus radius for s-orbitals.
B) number of peaks in radial probability distribution function versus radius is more than as in probability density versus radius of orbitals other than s-orbitals
C) number of peaks in radial probability distribution function versus radius is more than as in probability density versus radius of s-orbitals
D) number of peaks in radial probability distribution function versus radius is less than as in probability density versus radius of orbitals other than s-orbitals